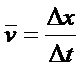Ch 15 – Fluid Mechanics

15.1 Density

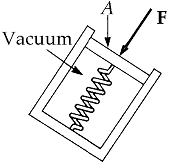
P = | F / A |      or P dA = dF SI units of Pressure is the Pascal 1 Pascal = 1 N / m^2 Density, ρ  (The Greek, r,  rho)      ρ = m / V

Some common densities

Important Note: If you notice, air (and other gasses) are approximately 1000 times less dense than liquids and solids

material

cgs

mks

Water

1

1,000

Ice

0.917

917

Air

0.00129

1.29

Helium (He)

0.00018

0.179

Copper (Cu)

8.96

8,960

That means the spacing between molecules is 10 times greater in all three dimensions (lxwxh) à (10x10x10=1000)

Gold (Au)

19.3

19,300

Platinum (Pt)

21.4

21,400

Iridium (Ir)

22.4

22,400

Aluminum

2.7

2,700

Lead (Pb)

11.34

11,340

Mercury (Hg)

13.6

13,600

Example using density The spring constant of the pressure gauge is 1000 N/m, and the piston has a diameter of 2.00 cm.  As the gauge is lowered into water, what change in depth causes the piston to move in by 0.500 cm?

P = F/A;       F = PA where P = ρgh F = -kx;      and F = ρghA k    x        = ρ g h A h =   k      x      /     ρ     g       A h = 1000*0.005 / (1000(9.8)π0.01^2) h = 1.62 meters

15.2 Pressure

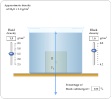
Pascal’s Law A change in pressure to a fluid is transmitted undiminished to every point of the fluid and to the wall of the container                       See bottom of page

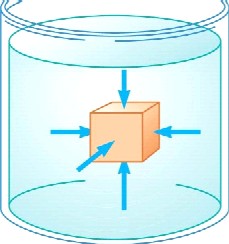
P1        =      P2 F1 /A1  =   F2 / A2 F1 A2           =    F2 A1 Pressure below a surface must include atmospheric pressure, Po,  as well pressure attributable to the liquid above, Pliq Fweight =  m   g             ρ =m/V;  m = ρV Fw     = ρ  V  g    Fw     = ρ(Ah)g   Fw     = ρ A h g Fw/A = ρ A h g /A Pliq    = ρ g h      h = depth of liquid P      = Po + Pliq Po = 1.013x10^5 Pa Pliq is also called Gauge Pressure

Application Pyramids of Egypt       P1               =      P2      F1 /A1          =   F2 / A2  ρstone hstone g    = ρH20  h  g  2500 (2) g       = 1000 h g         h              = 5 meters So the water column must remain 5 meters higher than the stone block

Tubes have been found below the pyramids of Egypt to a central chamber, possibly leading to a dried lake. If this is the case, one method to raise large stone blocks [(2x2x2) meters] is application of Pascal’s Law

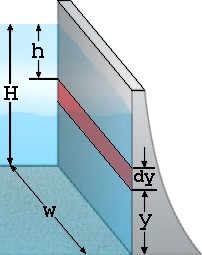
Example: Force on a dam with depth ΔF =       P         ΔA ΔF = ρ g (H-y)  wΔy  (use Calculus) F = ½ ρgwH^2 What is the force on a 80 meter wide dam which has a depth of 30 meters? F = ½     ρ    g   w   H^2 F = ½(1000)10(80)30^2 F = 360 MN or the same weight as 15,000 SUVs

Pressure readings referenced in every day usage generally is commonly referred to as gauge pressure. (i.e. 32 pounds / in^2 in our car tires.  This is 32 lb/in^2 beyond atmospheric pressure) Absolute pressure (P) is atmospheric pressure (Po) plus gauge pressure (ρ g h) P = Po + ρ g h

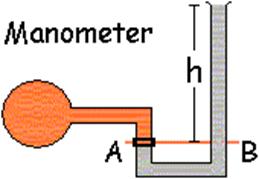
The key to the manometer is that the place of attachment, point A, is at the same level of the beginning measurement of h. Points A & B must be at same pressure, (at same level), so ρgh is the gauge pressure.

Common units of pressure

Compared to Po (1 atm)

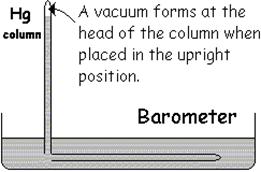
If the outside pressure goes higher … the surface of the Hg is pushed down even more…so the Hg in the column is pushed up in the column more. Vise versa if the outside pressure goes down.

Atmosphere

1 atm

Hg column

760 mm

Torr

760 torr

Pascal

1.013 x 10^5 Pa

Bar

1.013 bar

Mbar

1013 mbar

lb/in^2

14.7 lb/in^2

The above Mercury column experiment is a very powerful demo.  But we don’t perform this demo because Hg is a hazardous chemical.  So we instead we decide to use water.  Is this feasible in our classroom?

P  + ρgh    = Po + ρgh 0 + ρgh     = Po + 0             h is 0 meters above the surface ρgh          = Po h              =      Po       /    ρ          g h              = 1.013x10^5 / (1000) (9.8) h              = 10.3 meters

15.3 Static Equilibrium in Fluids: Pressure and Depths

Covered above and below in 15.6

15.4 Archimedes’ Principle and Buoyant Forces

The buoyant force on an object is equal to the weight of the displace fluid

Everyone should cover this subject during lab class. After all labs are complete, we will review this subject. Common topics usually covered during lab class are Bermuda triangle vanishing ships Underwater weight lifting using gold and aluminum weight sets Hot air balloons Archimedes and the King with the golden crown And more

The volume of the displace fluid is V If the displace fluid is water then the weight of the displaced water is m g = (ρH2OV) g à so  FB = (ρH2OV) g So if a crown displaces 30 cc’s of water (cc = cm^3, also cc = ml and 1 cc of water has the mass of 1 gram) FB = (   ρH2O *    V   )      g FB = (1 g/cc * 30cc) 1000 cm/s^2 (I usually use g = 10 m/s^2 or 1000 cm/s^2 during lecture) FB = 30,000 dynes  or FB = 0.3 Newtons    (100,000 dynes = 1 Newton) Active Figure 14.10

Archimedes Principle: Buoyancy

15.5 Application of Archimedes’ Principle

Bouyancy force…just sum up vectors… You see that there is a FNet up.

Covered in lab…if any more examples desired, please request during class

15.6 Fluid Flow and Continuity

There are two main types of fluid flow. · Steady (laminar) · Turbulent Viscosity measures the internal friction of a fluid (i.e. Elmer’s glue has more internal friction than water) To be able to model real fluids we must make a few assumptions (which usually are completely true). · The fluid is non-viscous · The fluid is steady · The fluid is incompressible · The fluid has no rotation

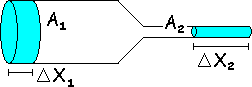
Equations Vcyclinder = A * x;     ρ = m / V;    V1 = A1 * x1                       V2 = A2 * x2 ρ = m1 /   V1 ρ = m2 /   V2 ρ = m1 / A1 x1 ρ = m2 / A2 x2 Δx1 = v1 Δt                               Δx2 = v2 Δt ρ = m1 / A1v1t1 ρ = m2 / A2v2t2 Since density of water is the same in both equations, we can set the two equations equal to each other m1 / A1v1t1        =   m2 / A2v2t2 A2v2  (m1/ t1)    =   A1v1  (m2/ t2)  ß Now let’s look at the example to the left. The mass per unit time was constant in either the wide part of the river or when the river flowed through the gorge.            (It was 40,000 kg / min) Since m/Δt is constant m1/Δt = m2/Δt and the equation simplified down to A1v1 = A2v2

A wide river with a flow rate of 10,000 gallons per minute (gpm) suddenly narrows.  What occurs? ans:  the water flows at a much faster velocity Most everyone already knew this answer from watching TV, movies, or other personal experience.   Why?  The 10,000 gpm still must flow at the same rate to make it through the gorge.  If the 10,000 gpm doesn’t flow at 10,000 gpm, it backs up and forms a lake behind the gorge. Just for fun… the mass of 1 gallon of water is approximately 4 kg.  So what is the mass of water flowing out of the gorge? 10,000 gal/min (4 kg/gal) = 40,000 kg/min

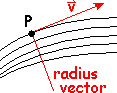
One last note on a particle in Laminar flow. The path taken by a fluid under steady flow is called a stream line (block lines), these form curves (parts of multiple circles).  Thus the velocity vector is tangent to each one of these stream lines.  I’m showing one velocity vector at point P.

Example: The channel at the Aquaduct at Segovia (Spain) has a channel that measures 1.5 wide by 1.8 tall measured in meters.  Immediately before the aquaduct is broken by a severe earthquake (fictional event) the water was flowing at 10cm/sec while being 1/3 full, what is the diameter of water stream when it reaches the ground 28 meters below?

Water volume per unit time is 1.5m (1/3*1.8 m) (0.1 m/s) V/t = 0.09 m^3/sec

Or Area (velocity) 1.5m (1/3*1.8 m) (0.1 m/s) A v = 0.09 m^3/sec

V / t = Af  vf 0.09 = Af (23.6) Af = 0.0038 m^2 πr^2 = 0.0038 r = 3.5 cm

Energy of position transfers to energy of position ½mv^2 = mgh v^2 = 2(10m/s^2) 28m vbottom = 23.6 m/s

Bernoulli’s Atomizer FM-C-BA

15.7 Bernoulli’s Equations

Bernoulli's Beach Ball FM-C-BB

Derivation: P1 – P2

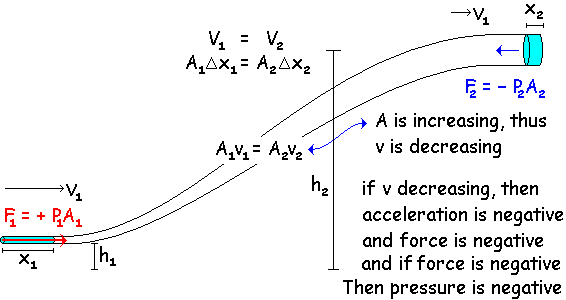
It’s already been established that pressure is measured in N / m^2; and volume is measured in m^3    So what are the units of PV (as in PV = nRT)? N / m^2 *  m^3  = Nm (units of Work and energy) So just from the units we expect:  Work = Δ P V Let’s look at this from another view point Work = F Δx Work = F Δx (A / A)                multiplying by 1 Work = (F/A)  (Δx A) Work = Δ P          V          …very similar to above. So we can conclude that a change in pressure for a constant volume is the amount of work done on a system.

So if pressure is changed, you do work Work = P1V + (– P2V) &      Work = ΔK           But what if the pipe slopes up or down.           Gravity will also do work on the system. Work = ΔK + ΔU P1V – P2V = ½mv2^2 – ½mv1^2 + mgh2 – mgh1 P1V + ½mv1^2 + mgh1 =  P2V + ½mv2^2 + mgh2           So final equals initial…or no changes…so PV    + ½mv^2      + mgh               =  constant Divide through by volume P      + ½(m/V)v^2       + (m/V)gh   =  constant P      + ½ρv^2+ ρgh        =  constant

15.8 Applications of Bernoulli’s Equation

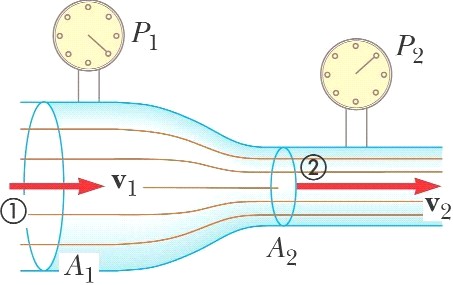
A Venturi tube may be used as a fluid flow meter.  If the difference in pressure is P1 – P2 = 21.0 kPa, find the fluid flow rate in cubic meters per second, given that the radius of the outlet tube is 1.00 cm, the radius of the inlet tube is 2.00 cm, and the fluid is gasoline (ρgas = 700 kg/m^3).

Ain   = π(2)^2;       Aout  = π(1)^2       Ainvin = Aoutvout       4  vin =   1  vout vout = 4vin

P      + ½ρv^2  + ρgh   =  Pf + ½ρvf^2 + ρghf Pin     + ½ρvin^2             =  Pout + ½ρvout^2 Pin - Pout    + ½ρvin^2     =    ½ρ vout^2 21,000      + ½ρvin^2     =    ½ρ(4vin)^2 15vin^2                        = (2/ρ) 21,000 vin = 2 m/s

Venturi Tube

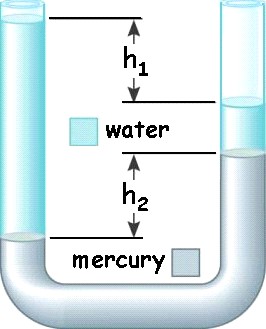
Another example to the right… So what is h2? Hint: What is the weight of the two columns?

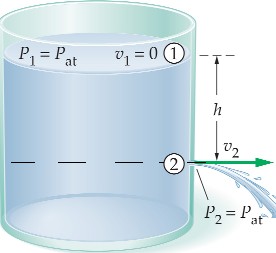
What is v2? P      + ½ρv^2  + ρgh = P2   + ½ρv2^2 + ρgh2 Pat    + 0      + ρgh = Pat  + ½ρv2^2   + 0 ρgh    =  ½ρv2^2 v2^2 = 2gh This results is Torricelli’s Law

Last Application…

15.9  Viscosity and Surface Tension

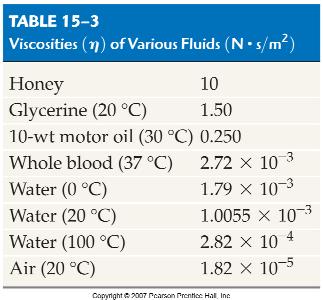
We have ignored internal friction (like usual), but how would our discussion change if we didn’t? As with surface friction, friction that fluid experiences is also ALWAYS opposed to its flow (come speak to me if you don’t agree with “always”, if you don’t believe this, it comes from a misinterpretation of the definition of a system) P1 – P2 = 8πη v L / A; where eta is the coefficient of viscosity W Viscosity was originally measured in poise where water at 20°C was 0.01 poise (dyne sec/cm^2).  We use SI units (see table). 1 poise = 0.1 Ns/m^2 Multiply both sides of the above equation and solve for vA vA = (P1 – P2)A^2 / 8πηL     (remember V/t = vA)