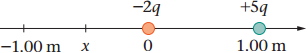Ch 20 Electric Potential (and Energy)

Electric Potential and Potential Energy

Work is required to move an electric charge perpendicular to an electric field.  Electric Force is conservative.

· Ch 7 à Work = F_applied Δx

· Ch 19  F = qE

· So we know Work = q E Δx    OR

· Work = -q E d 

o à Remember, lines of force in an electric field start at positive and end at negative conductor

· ΔU = -Work

· ΔU = q E d 

· U = q (k  q / r²) d

· U = k  q / r

Change in electric potential energy

ΔU = -W

Electric Potential àvolts

· ΔV = ΔU / q₀

· ΔV = -W / q₀

**New definition

Electron Volt – the amount of energy required to move one electron through a potential difference of one volt.

· 1 eV = 1.6 x 10¹⁹C (1V)

· 1 eV = 1.6 x 10^-19 Joules

· Referring back to explanation in Ch 19

· E = - ΔV / Δx

· The greater the change in voltage per unit distance, the greater the electric field.

Example

When an ion accelerates through a potential difference of -2000V , its electric potential energy decreases by 10⁻¹⁶ J.  What is the charge on the ion?

Work  = - q ΔV

10^-15 Joules = -q (-2000 V)

q = 5 x 10^-19 Coulombs

Energy Conservation

· Don’t forget PHY121

· TE_initial               = TE_final

· PE_o   +   KE_o       = PE_f   +   KE_f

Or

· U_o    +     K_o       =   U_f    +  K_f

· mgh_o + ½ mv_o²    = mgh_f + ½ mv_f²

For electric force à U = qV

Potential Energy is in  many forms, height or gravitational, springs, magnetic fields (Inductors), electrostatic field (capacitors), etc

Also don’t forget from earlier

• Since the force on a negative charge is opposite to the field direction:

– Positive charges accelerate in the direction of decreasing electric potential.

– Negative charges accelerate in the direction of increasing electric potential.

• In both cases, the charge moves to a region of lower potential energy.

Example

A diode consists of two electrodes within a highly evacuated typically cylindrical coaxial enclosure. The cathode, is maintained at a high temperature and emits electrons from its surface. A potential difference of a few hundred volts is maintained between the cathode and the anode, with the anode at the higher potential. The cathode on the inside cylinder has a radius of 0.1000 cm and the outside shell, the anode, has a radius of 0.5000 cm . The potential difference between the anode and cathode is 200 V.  Find final speed of the electron when it strikes the anode, assuming initial speed ~ 0 m/s?

· q = 1.6x10^-19 V

· m = 9.11x10^-31 kg

E = qV = ½mv²

v = (2 qV/m)^½

v = 8.38 x 10⁶ m/s

Note:  what about the inner shell and outer shell radius?

Electric Potential of Point Charges

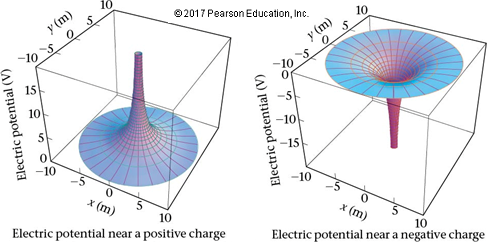
· So what is the electric potential of a point charge?

ΔV =  ΔU     /  q₀

V = k q₀ q / r / q₀  for a point charge

o Answer:  V = k q / r

· Remember… we know

o F/q = E = k |q|/ r²

o ΔU = q     E      d 

o U = k q₀ q / r

o And last but not least

o ΔV = ΔU    /  q₀ à electric potential

Example

Find the value of x between −1.00 m and 0 where the electric potential is zero.

(a) 2q /(x) = 5q / (1+x)

· -3x = 5

· x = -0.667 m

(b) At values of x to the left of −1.00 m, do you expect the electric potential to be greater than, less than, or equal to zero?

· Greater than à extremely further to the left -2q and 5q, merges to 3q.

(c) Calculate the electric potential at x=−4.00m, when q = 4x10^-9 C?

· V = k    (q₁ / r₁   +   q₂ / r₂)

· V = k   (-2q/ 0--4 + 5q/ 1--4)

· V = 9e9(4e-9)(-½ + 5 /    5)

· V = 18 Volts

Equipotential Surfaces and the Electric Field

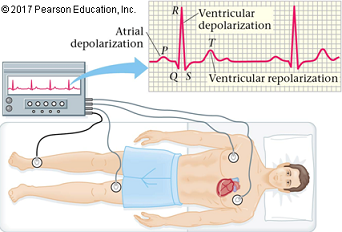
• There are electric fields inside the human body; the body is not a perfect conductor, so there are also potential differences.

• An electrocardiograph (ECG) plots the heart’s electrical activity

• An electroencephalograph (EEG) measures the electrical activity of the brain:

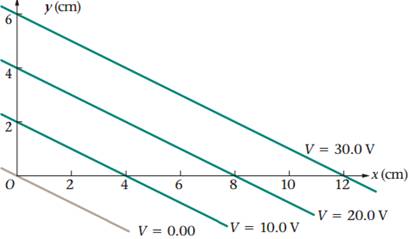
Example

· V = 0;  y = -1/2 x

· V = 10;  y = -1/2 x + 2

· V = 15;  y = -1/2 x + 3

· V = 17.5;  y = -1/2 x + 3.5

· V = 20;  y = -1/2 x + 4

· V = 30;  y = -1/2 x + 6

· V = 40;  y = -1/2 x + 8

(a) What is electric potential at (1,3)

· (3) = -1/2 (1) + 3.5

· V = 17.5

If more difficult then we must calculate the y-int…         

  y  =     m     x   + b

(3) = -1/2 (1) + b

y-int = 3.5, which corresponds to

àV = 17.5;  y = -1/2 x + 3.5

(b)   How much work is done by the electric force when a 0.50-C charge is moved from the point (1.0 cm, 3.0 cm) to the point (12.0 cm, 2.0 cm)?

Ø Potential at (12,2) is  V = 40

o satisfies this equation

o à y = -1/2 x + 8

Ø Work =    - q       (ΔV)

Ø Work = -( ½ C) (40-17.5)

Ø Work = -11.25 Joules

Capacitors and Dielectrics

• A capacitor is two separated (traditionally) parallel conducting plates

• Also called a parallel plate capacitor

•     C   =    Q    /   V

• Farad = charge / volt ß  units

• Recall:    E = σ  / ε₀

• Recall:    σ = q / A

• Recall:    E = - ΔV / Δx

• C =  ε₀ A / d

Dielectrics

C_o = q / V_oà  V_o = E_o d

E in a dielectric = E_o / κ

· κ_{vacuum or air}  = 1

· κ_paper         = 3.7

· κ_rubber        = 6.7

· κ_water         = 80

· κ_plastic        = 2 to 4

· κ_{Sr Titanate}    = 233

V = E d = (E_o/κ) d = V_o /κ

C = Q  /  V

C = Q / (V_o/κ) = κC_o

C = κε₀ A / d

Example

A capacitor with plate area 0.060 m²and plate separation 60.0 μm is to be charged to 12.0 V and store 8.85 μJ of energy.  What should be the dielectric constant of the material between the plates? 

U = ½ C V² where C = κε₀ A / d

κ = 2 (d) U / ε₀ A V²

2*60x10^-6 (8.85x10^-6)	= 13.9
8.85x10^-12(.0600) 12^2

Electric Energy Storage

· U = QV_ave

o V_ave = ½(V_o + V_max)

· U = ½ Q V_max

o Q = C V

· U = ½ C V²

o Or½ Q²/C

• Recall:    E = σ  / ε₀

• Recall:    σ = q / A

• Combine:  Q = ε₀ E A

• Recall:    V = E d

U = ½ Q V

U = ½ ε₀E AE d

U = ½ ε₀E² Ad

U = ½ ε₀E² Vol

Electric Energy Density = Energy   / Volume

Electric Energy Density =½ ε₀E² Vol / Vol

Electric Energy Density = ½ ε₀ E²

Example

The membrane of a living cell can be approximated by a parallel-plate capacitor with plates of area 5.00 x 10⁻⁹ m², a plate separation of 10 x 10⁻⁹ m, and a dielectric with a dielectric constant of 4.0.

a. What is the energy stored in such a cell membrane if the potential difference across it is 7.00 x 10⁻² V  

b. What would occur if the thickness of the cell membrane is increased

i. Increase

ii. Decrease

iii. Stay the same

c. Explain

(a)

U =  ½ κ      ε₀        A   V²    / d

U = ½ 4(8.85e-12)(5)(.07)² / 10

U  = 4.34×10⁻¹⁴ J

(b) Decrease

(c)

Because U ~ 1/d the answer to part A would decrease if the thickness of the cell membrane is increased.

Note:  the membrane is the wall thickness, not the cell diameter