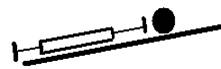
Ch 7.2             #3

Batman, whose mass is 80 kg, is holding onto the free end of a 12 m rope, the other end of which is fixed to a tree limb above.  He is able to get the rope in motion as only Batman knows how, and eventually getting it to swing enough so that he can reach a ledge when the rope makes a 60° angle with the vertical.  How much work was done against the force of gravity in this maneuver?

cos 60° = Δy / hyp Δy = 12m * cos 60° Δy = 6 m

Ug =  mgh Ug =  80 kg * 10 m/s^2 * 6 m Ug =  4800 Joules

Ch 7.3             #7

A force F = (6i – 2j) N acts on a particle that undergoes a displacement of Dr = (3i + j) m.

Find (a) the work done by the force on the particle and (b) the angle between F & Dr

(a)      Work = ∫F dr (x&y are independent)		(b)
Wx = ∫Fx dx	Wy = ∫Fy dy
Force isn’t dependant upon position so		|F| = (Fx^2 + Fy^2)^½ |F| = 6.32 N	|d| = (dx^2 + dy^2)^½ |d| = 3.16 m
Wx = Fx Δx	Wy = Fy Δy
Wx = 6 * 3 Wx = 18i	Wy = -2 * 1 Wy = -2j	Work = F•d cosq 16J    = 6.32*3.16 cosq q        = 36.8°
Work = 18 – 2           Work = 16 Joules

Ch 7.4             #14

A force F = (4x i + 3y j)Newtons acts on an object as the object moves in the x dir from the origin to x = 5.00 m.  Find the work done on the object.             Work = ∫F∙dr.

The y component is orthogonal no work in the vertical direction Work = ∫F∙dr

Work = 4∫xdx from 0 to 5 Work = 4 ½x^2 from 0 to 5 Work = 2 * 5^2 = 50 Joules

Ch 7.4             #19

It takes 4 J of work to stretch a Hooke’s Law spring 10 cm from its unstressed length, determine the extra work required to stretch it an additional 10 cm.

Work           = ½ k xi^2       - ½ k xf^2 4 J    = 0               - ½ k (-0.1 m)^2 k = 800 N/m

Work = ½ k xi^2       - ½ k xf^2 Work = ½ k 0.1^2      - ½ k 0.2^2 Work = ½ 800 (0.01 – 0.04) Work = -12 J in addition

Remember Hooke’s law is referenced to restoring force…so a positive number is returning to its original position.

Ch 7.6             #26

A 3kg object has a velocity of (3i - 2j) m/s.  (a) What is the kinetic energy at this time?

(b) Find the total work done of the object if its velocity changes to (8i + 4j) m/s

(a) KE is not directional v^2 = (vx^2 + vy^2) K = ½m(vx^2 + vy^2) K = ½3 (3^2 + (-2)^2) K = 19.5 J

(b)     Kf = ½m(vx^2 + vy^2)           Kf = ½3 (8^2 + 4^2)           Kf = 120.0 J Work = ΔK Work = 120 J – 19.5 J Work = 100.5 Joules

Ch 7.8             #40

A 650 kg elevator starts from rest.  It moves upward for 3 s with constant acceleration until it reaches its cruising speed of 1.75 m/s.  (a) What is the average power of the elevator motor during this period?  (b) How does this power compare with its power when it moves at its cruising speed?

a = Δv / Δt a = 1.75 m/s / 3 s a = 0.5833 m/s^2 d = ½ at^2 d = 2.625 m

ΔKE = ½ mv^2 ΔKE = ½ 650 1.75^2 ΔKE = 995 Nm Work = ΔK + Ug Work = 995+650g*2.625 Work = 17716 Nm

Or Work = 650*(g+a)*2.625 Work = 17716 Nm Power = Work / time Power = 17716 / 3 Power = 59005 J

(b) At cruising speed P = Work / Δt P = Fw * d / Δt P = 650g * 1.75*3 / 3 P = 11150 Joules

Ch 7.9             #45

A compact car of mass 900 kg has an overall motor efficiency of 15%.

(a) if burning one gallon of gasoline supplies 1.34 x 10⁸ joules of energy, find the amount of gasoline used in accelerating the car from rest to 55 mph. (ignore air friction and rolling friction)

(b) How many such accelerations will one gallon provide?

(c) The mileage claimed for the car is 38 mpg at 55 mph.  What power is the delivered to the wheels (to overcome friction) when the car is driven at this speed?

                                    55 miles / hr *1609 m / mile * 1 hr / 3600 sec = 24.57 m/s

(a)Work       = ½ m (vf – vi)^2 Work                    = ½ 900 (24.59)^2 Work                    = 2.72 x 10^5 Joules Only 15% efficient             Estartup = 2.72 x 10^5 J / 15%             Estartup = 18.1 x 10^5 J Given: E1 gallon = 1.34 x 10^8 joules Estartup / E1 gallon  = 18.1x10^5J / 1.34x10^8J Percentage = 1.35% of a gallon	(b)     (1.34 x 10^8 J / gal) / (18.1 x 10^5 J / accel)           = 73.8 start ups
	(c)      Power = Work / time * efficiency 55mph (1h/3600s) (1 gal/38 miles) * (1.34x10^8 J/gal) * 50%           = 8.08 kW

Ch 7                 #63

The ball launcher in a pinball machine has a spring that has a force constant of 1.2 N/cm.  The surface on which the ball moves is inclined 10°.  If the spring is initially compressed 5 cm, find the launching speed of a 100g ball when the plunger is released.

Workspring                   -          Workgravity                  = DKE ½ k xi^2 - ½ k xf^2         -          mgh                             = DKE ½(120 N/m)(.05 m)^2             – sin10°(.05 m)(.1 kg)(10m/s^2) = ½ (.1 kg)vf^2 vf = 1.68 m/s

Ch 7.5             (#39 in 5^th edition, not in 6^th edition)

A bullet with a mass of 5 g & speed of 600 m/s penetrates a tree to a depth of 4 cm.  (a) Use work and energy considerations to find the average frictional force that stops the bullet.  (b) Assuming that the frictional force is constant, determine how much time elapsed between the moment the bullet entered the tree and the moment it stopped.

Worktree      = ΔKE -Ffrict Δx      = ½ mvf^2       – ½ mvi^2 -Ff (0.04m)  = 0 - ½ (0.005kg) (600m/s)^2 Ff                = 22500 N

(b) vave              = Δx            / Δt 300 m/s       = 0.04 m      / Δt t = 0.000133 seconds

Ch 7                 #60

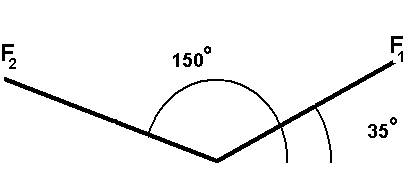Two constant forces act on a 5 kg object moving in the x-y plane.  Force F₁ is 25 N at 35 degrees while F₂ = 42 N at 150 degrees.  At time t = 0, the object is at the origin and has velocity of (4 i + 2.5 j) m/s.  (a) Express the two forces in unit-vector notation.  Use unit-vector notation for your other answers. (b) Find the total force on the object.  (c) Find the object’s acceleration.  Now considering the instant t = 3s, (d) find the object’s velocity (e) its location (f) its kinetic energy from ½ m v_f², and (g) its kinetic energy from ½ m v_i² + å F ×d.

(a) F₁:  cos 35° * 25 N i + sin 35° * 25 N j

            F₁:        (20.5 i + 14.3 j) N

F₂:        -cos 30° * 42 N i + sin 30° * 42 N j

            F₂:        (-36.4 i + 21.0 j) N

(b) F₁ + F₂ = (-15.9 i + 35.3 j) N = (38.7 N @ 114.2°)    

(c) F = m a       -15.9 N = 5 kg * a_i         a_i = -3.18 m/s²

35.3 N = 5 kg * a_j         a_j = 7.07 m/s²

(-3.18 i + 7.07 j) m/s²

(d)                   a_x = Dv_x / Dt;                -3.18 = (v_f – 4) / 3 = v_f = -5.52 i

a_y = Dv_y / Dt;                 7.07 = (v_f – 2.5) / 3 = v_f = 23.7 j

or (-5.52 i + 23.7j) m/s

(e)     d_x =  v_o t + ½ a t² = 4 (3) + ½ -3.18 3² = 12 + 14.31 = -2.31 m

d_y =  v_o t + ½ a t² = 2.5 (3) + ½ 7.07 3² = 7.5 + 31.8 = 39.3 m

or (-2.3i + 39.3j) m

(f)      KE = ½ m v_f² = ½ 5 (23.7^2+5.52^2) = 1480 J

(g)       Use Definition for work: Work =  åF·d = DKE = ½ mv_f² – ½ mv_i²             Solve for ½ mv_f² = åF·d + ½ mv_i²

Thus the exact same as (f)