Ch 19 – Heat Engines, Entropy, & 2^nd Law of Thermodynamics

Heat Engines and the 2^nd Law of Thermodynamics

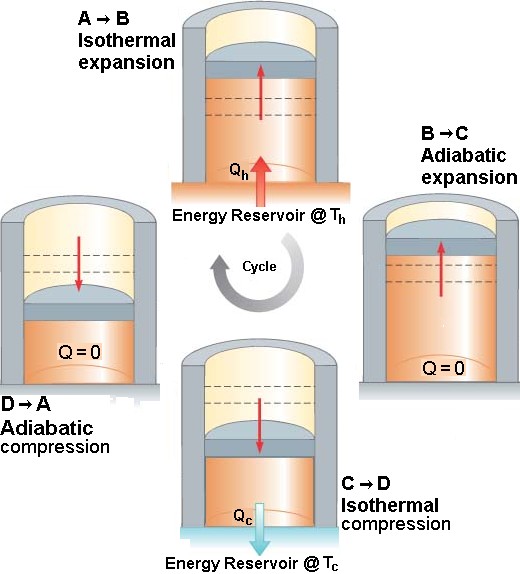
A heat engine is a device that take an energy input through heat an does a fraction of the input energy as work as a cyclic process

A sterling engine A steam locomotive Automotive engine etc

A heat engine carries some working substance through a cyclic process during the working substance absorbs energy by HEAT from a high temp energy reservoir work is done by the engine energy is expelled by heat to a lower-temp reservoir

Suppose a heat engine is connected to two energy reservoirs, one a pool of molten aluminum (660°C) and the other a block of solid mercury (–38.9°C). The engine runs by freezing 1.00 g of aluminum and melting 15.0 g of mercury during each cycle. The Lf of Al is 3.97 x 105 J/kg; Lf of Hg is 1.18 x 104 J/kg. What is the efficiency of this engine?

Heat required to melt 15.0 g of Hg Q = m Lf Q = 0.015 (1.18x104) Qc = 177 Joules

Energy absorbed by 1.00 g of aluminum Q = m Lf Q = 0.001(3.97x105) Qh = 397 J

the work output Wengine = Qh – Qc Wengine = 397-177 Wengine = 220 J

eff = Wengine / Qh eff = 220 / 397 eff = 55.4%

The theoretical (Carnot) efficiency is effmax = 1 – TC/TH effmax = 1 – (273.15-38.9) / (273.15+660) effmax = 74.9%

Demo: Stirling Engine: TH-F-SC http://www.stirlingenergy.com/breaking_news.htm

Heat Pumps and Refrigerators

A heat pump transfers energy from a cold to a hot reservoir. We must add energy to accomplish this process. Other common names, air conditioner, refrigerator, etc.

For heating mode COP(heater) = Qh / Work

For cooling mode COP(refrig) = Qc / Work Good refrigerators have a coefficient of performance, COP, of about 6

Clausius statement Energy does NOT transfer spontaneously by heat from a cold object to a hot object!

Example A refrigerator has a coefficient of performance equal to 5.00. The refrigerator takes in 120 J of energy from a cold reservoir in each cycle. Find (a) the work required in each cycle and (b) the energy expelled to the hot reservoir.

a. COP(refrig) = Qc / Work 5.00 = 120 J / Work Work = 24.0 Joules b. Heat expelled = Heat removed + Work done Qh = Qc + Work Qh = 120 + 24 Qh = 144 Joules

Reversible and Irreversible Processes

A reversible process the system undergoing the process can be returned to its initial conditions along the same path on a PV diagram. Also every point along this path is an equilibrium state.

An irreversible process is a process that does NOT satisfy these requirements. All REAL processes are IRREVERSIBLE!!!

Some real processes are almost reversible. If a real process occurs very slowly such that the system is almost in an equilibrium state, then the process can be approximated as being reversible. A gas is compressed isothermally in a piston which is in contact with the energy reservoir, so that energy transfer will keep the temp constant.

Almost like your Ideal gas lab if insulated and sealed. As you add the weights in very small increments and then remove the weight just a slowly, the cylinder will return to its initial position. (Why insulated…if not then the increased temperature in the bottle form compression will be transferred to the environment).

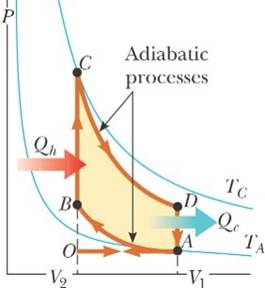
The Carnot Engine

Carnot’s theorem – No real heat engine operating between two energy reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs.

What is the coefficient of performance of a refrigerator that operates with Carnot efficiency between temperatures –3.00°C and +27.0°C? COPrefrig = TC / ∆T COPrefrig = (273.15 + -3) / 30 COPrefrig = 9

Example A heat engine operating between 200°C and 80.0°C achieves 20.0% of the maximum possible efficiency. What energy input will enable the engine to perform 10.0 kJ of work?

The Carnot efficiency of the engine is effc = ∆T / Th effc = (200-80) / (273.15+200) effc = 25.3%

If 20% efficient we only get 25.3% * 20% = 5.06% eff = Wengine/ Qh 5.06% = 10 KJ / Qh Qh = 197 KJ

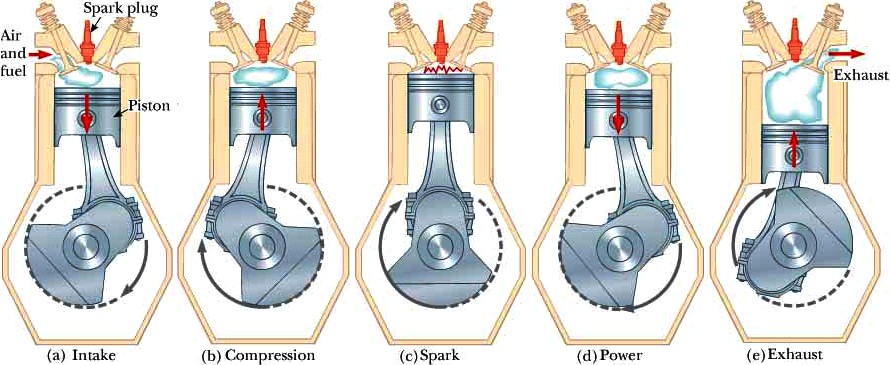
Gasoline and Diesel Engines

Intake stroke O à A Compression stroke A à B Combustion B à C Power stroke C à D Exhaust opens D à A Exhaust stoke A à O If we assume an ideal gas, then the efficiency of the Otto cycle is e = 1 – 1/(V1/V2)^γ^-1 Or e = 1 – (V1/V2)^1-^γ

Chemical PE In Positive Work on gas PE to Qh Gas expands adiabatically P drops suddenly V drops V1 to V2 γ = CP/CV where V1/V2 is the compression ratio

Example A gasoline engine has a compression ratio of 6.00 and uses a gas for which = 1.40. (a) What is the efficiency of the engine if it operates in an idealized Otto cycle? (b) What If? If the actual efficiency is 15.0%, what fraction of the fuel is wasted as a result of friction and energy losses by heat that could by avoided in a reversible engine?

effotto = 1 – (V2 / V1)^γ^-1 effotto = 1 – (1 / 6)^1.4 - 1 effotto = 51.2% losses = effotto - effactual losses = 51.2% - 15% losses = 36.2%

Entropy

Entropy is a measure of disorder in isolated systems. Entropy is another state variable of 2^nd law of thermodynamics

Microstate: a particular configuration of the individual components (orientation, spin states, directions at one point of time, etc) Macrostate: a description using the state variables (P, T, ρ, etc)

Far more macrostates exist with disordered microstates than with ordered microstates, i.e. there is only one microstate where all the vectors are pointing to the left. Thus macrostates are always moving toward disorder.

dS = dQr/T ∆S = ∫dS ∆S = ∫ dQr / T ∆S = |Qh|/Th - |Qc|/Tc For a Carnot engine operating in a cycle |Qh|/Th = |Qc|/Tc Thus ∆S = 0 Now consider a non-Carnot but still reversible cycle. We still know ∆S = 0 So dQr / T = 0 (integral over a closed loop, you’ll see this a lot more in electrical physics when dealing with Ampere’s Law)

Quasi-Static, Reversible Process for an Ideal Gas Initial: Ti and Vi; Final: Tf and Vf dQr = dEint - dW dQr = dEint - (-PdV) dQr = nCvdT + nRT (dV/V) (divide by T) dQr / T = nCvdT/T + nR(dV/V) ∆S = ∫ dQr / T ∆S = ∫nCvdT/T + ∫nR(dV/V) ∆S = nCv ln(Tf/Ti) + nR ln(Vf/Vi)

Example An ice tray contains 500 g of liquid water at 0°C. Calculate the change in entropy of the water as it freezes slowly and completely at 0°C.

For a freezing process, change of entropy, ∆S = ∆Q / T ∆S = -mLf / T ∆S = -.5(3.33x10^5)/273.15 ∆S = -610 J/K

Entropy Changes in Irreversible Processes

The total entropy of an isolated system that undergoes a change CANNOT decrease In irreversible processes Entropy always increases In reversible processes (non-real processes) ∆S is constant

Entropy in free expansion (no pressure increase) dS = dQr/T ∆S = 1/T ∫(nRT/V) dV ∆S = nR ∫(1/V) dV ∆S = nRln(Vf/Vi)

Entropy Change in Calorimetric Processes Tf = (m1c1Tc + m2c2Th) / (m1c1 + m2c2) dS = dQc/T ∆S = m1c1 ln(Tf/Tc) + m2c2 ln(Tf/Th)

The temperature at the surface of the Sun is approximately 5700 K, and the temp at the surface of the Earth is approximately 290 K. What entropy change occurs when 1000 J of energy is transferred by radiation from the Sun to the Earth?

∆Ssystem = ∆(Q / T) ∆Ssystem = ∆(1000/290 – 1000/5700) ∆Ssystem = 3.27 J/K

Entropy on a Microscopic Scale

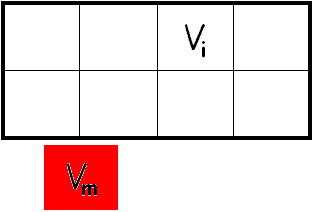
Let Vi be the initial volume for a given gas. Let Vm be the size of the molecule (;the volume the molecule occupies) A 2-D representation is to the right.

How many different ways is VM allowed? Ans…eight How do we arrive at this numerically?

Ans: Vi = 8 units; Vm = 1 unit w1 = Vi / Vm w1 = 8 units / 1 unit w1 = 8

What if Vi is 10^23 cubic units? This means if another particle of size VM is added is also has w2 different allowed positions or ways. So what is the total # of ways of positioning these two particles in the original volume? W = (w1)(w2) Add a third particle…so the different ways of positioning will be W = (w1)(w2)(w3) where w1 ≈ w2 ≈ w3 Or W = w1^3 So a formula for determine total number of ways for positioning particle is Wi = wi^N Wi = (Vi / Vm)^N

And for final volume Wf = (Vf / Vm)^N Set a ratio of final to initial Wf / Wi = (Vf / Vm)^N/ (Vi / Vm)^N Wf / Wi = (Vf / Vi)^N ln(Wf / Wi) = (N) ln(Vf / Vi) kB ln(Wf / Wi) = kB (N) ln(Vf / Vi) kB ln(Wf / Wi) = kB(nNA)ln(Vf / Vi) kBln(Wf) - kB ln(Wi) = n(kBNA)ln(Vf / Vi) kBln(Wf) - kB ln(Wi) = n (R) ln(Vf / Vi) We also know from 22.7 Entropy Change in Free expansion is Sf - Si = n (R) ln(Vf / Vi) Thus Sf - Si = kBln(Vf) - kB ln(Vi) Or ΔS = kB ln(Work)

If you toss two dice, what is the total number of ways in which you can obtain (a) a 12 and (b) a 7?

2 3 4 5 6 7 8 9 10 11 12 1,1 1,2 1,3 1,4 1,5 1,6 2,1 2,2 2,3 2,4 2,5 2,6 3,1 3,2 3,3 3,4 3,5 3,6 4,1 4,2 4,3 4,4 4,5 4,6 5,1 5,2 5,3 5,4 5,5 5,6 6,1 6,2 6,3 6,4 6,5 6,6 1 2 3 4 5 6 5 4 3 2 1

As you can see…only one combo will give you a 12; (6,6) And a 7 can be obtained in 6 ways